↠A few very general scientific principles are needed to predict deformation and failure.
↠With very general principles, we can consider bodies with a wide range of geometries and materials, which are
subjected to many types of loads.
↠Mechanics of Materials introduces these principles and applies them to bodies and loadings that can be
analyzed with relatively simple mathematics.
1.Separate out the effects of material and geometry by viewing a body as composed of many tiny
elements.
↠Any body can be viewed as an assemblage of tiny, in fact infinitesimal, cubic elements. This insight allows us
to separate out the effect of the body’s material from its shape.
↠Since a tiny cube is a standard shape,the relations between the cube’s deformation and the forces on it depend only
on the material, for example, the particular type of ceramic, metal, plastic, or wood
These relations can be measured and described for a given material, and they are relevant to a body of any shape
and size composed of that material.
2.Relate forces and deformations at the element level with those at the level of the overall structure.
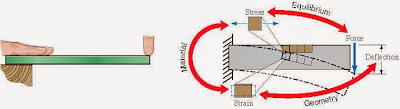
↠Mechanics of materials defines stress and strain to describe force and deformation at the level of an elemental
cube.
↠To determine a body’s overall deformation and potential for failure, we combine
(1) the material-specific stress–strain relations for a cubic element,
(2) equilibrium relations between forces on the body as a whole and the forces on its elements, and
(3) geometric relations between deformations of the whole body and of its elements.
3. Loaded bodies often deform in simple patterns, namely, stretching, twisting, or bending.
↠Engineers deal with deformation and failure in structures having a wide variety of shapes, materials, and loadings.
↠In mechanics of materials, we study deformation and failure primarily for simple patterns of deformation:
stretching, twisting, or bending.
↠For each pattern, the overall loading is described by equal and opposite forces or moments at the two ends.
↠The overall deformation is described by a single parameter: how much the body stretches, twists, or bends.
4. Study deflection and failure for each pattern individually, and then how they combine.
↠In mechanics of materials, we learn how the forces and deformations vary from one cubic element to another for
each deformation pattern . With that information, we interrelate the overall load and deformation for that pattern, and
we find the load at which failure will occur.
↠We learn how the body’s geometry (length and cross-section) and the body’s material independently affect the
overall deformation and failure.
↠Faced with applications that appear complex, we must also learn to detect the presence of these simple deformation
patterns, alone or, often, in combination. We typically analyze the deformations and stresses in each pattern and then
combine them appropriately to find the total deformation and to determine if failure will occur.
↠With very general principles, we can consider bodies with a wide range of geometries and materials, which are
subjected to many types of loads.
↠Mechanics of Materials introduces these principles and applies them to bodies and loadings that can be
analyzed with relatively simple mathematics.
1.Separate out the effects of material and geometry by viewing a body as composed of many tiny
elements.
↠Any body can be viewed as an assemblage of tiny, in fact infinitesimal, cubic elements. This insight allows us
to separate out the effect of the body’s material from its shape.
↠Since a tiny cube is a standard shape,the relations between the cube’s deformation and the forces on it depend only
on the material, for example, the particular type of ceramic, metal, plastic, or wood
These relations can be measured and described for a given material, and they are relevant to a body of any shape
and size composed of that material.
2.Relate forces and deformations at the element level with those at the level of the overall structure.
↠Mechanics of materials defines stress and strain to describe force and deformation at the level of an elemental
cube.
↠To determine a body’s overall deformation and potential for failure, we combine
(1) the material-specific stress–strain relations for a cubic element,
(2) equilibrium relations between forces on the body as a whole and the forces on its elements, and
(3) geometric relations between deformations of the whole body and of its elements.
3. Loaded bodies often deform in simple patterns, namely, stretching, twisting, or bending.
↠Engineers deal with deformation and failure in structures having a wide variety of shapes, materials, and loadings.
↠In mechanics of materials, we study deformation and failure primarily for simple patterns of deformation:
stretching, twisting, or bending.
↠For each pattern, the overall loading is described by equal and opposite forces or moments at the two ends.
↠The overall deformation is described by a single parameter: how much the body stretches, twists, or bends.
4. Study deflection and failure for each pattern individually, and then how they combine.
↠In mechanics of materials, we learn how the forces and deformations vary from one cubic element to another for
each deformation pattern . With that information, we interrelate the overall load and deformation for that pattern, and
we find the load at which failure will occur.
↠We learn how the body’s geometry (length and cross-section) and the body’s material independently affect the
overall deformation and failure.
↠Faced with applications that appear complex, we must also learn to detect the presence of these simple deformation
patterns, alone or, often, in combination. We typically analyze the deformations and stresses in each pattern and then
combine them appropriately to find the total deformation and to determine if failure will occur.



No comments:
Post a Comment