- Design of products, systems, and structures demands the engineer to consider a broad range of issues.
- The issues addressed by Mechanics of Materials are - excessive deformation and material failure.
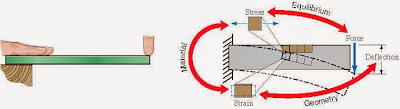
- We consider the body to be composed of elements, we study common deformation modes, and we combine contributions of each deformation mode, as needed,to assess deformation and failure.
 | |||
 | |||
 |  |  |
Issues addressed by Mechanics of Materials
1.Account for deformation and the potential for failure when designing systems subjected to forces.
Forces acting on designed artifacts can be significant. All bodies deform under applied forces,
and they can fail if the forces are sufficiently large.
Mechanics of Materials addresses two prime questions:
●How much does a body deform when subjected to forces?
●When will forces applied to a body be large enough to cause the body to fail?
Deformation and failure depend on the forces and on the body’s material, size, and shape.
2.Deformations within acceptable limits-
In most situations,we try to avoid failure and keep deformations within acceptable limits.
If we know the forces under which failure would occur, we can design to avoid failure. Further, a system often needs to remain close to its original shape to function properly. If we can quantify deformations, we can design the system to avoid undesirably large deformation.
3.Desirable deformation -
Deformation is desirable in some situations where it depends predictably on the forces.Some products must deform to carry out their function. They are designed to have a desired relation between the deformation and the acting forces.
For example, such products include pole vaults that flex to temporarily store energy that later propels the vaulter, mountings that accommodate motions of helicopter blades, and support springs that allow for deflection of structural members.



4.Desirable failure -
Occasionally, failure is desirable, if it occurs at a reproducible level of load.
Rarely, we sometimes deliberately want failure to occur when loads reach a predetermined level. In expensive equipment, failure can be disastrous. So, engineers design into the equipment an inexpensive extra part, which fails at a consistent force that is safely less than the main components can tolerate.
For the transmission shaft in a drive train, such a system that protects the shaft is called a torque fuse. Just as an old fashioned electric fuse breaks when the current is too high, the pins in the torque fuse break when the torque is too high.
Forces acting on designed artifacts can be significant. All bodies deform under applied forces,
and they can fail if the forces are sufficiently large.
Mechanics of Materials addresses two prime questions:
●How much does a body deform when subjected to forces?
●When will forces applied to a body be large enough to cause the body to fail?
Deformation and failure depend on the forces and on the body’s material, size, and shape.
2.Deformations within acceptable limits-
In most situations,we try to avoid failure and keep deformations within acceptable limits.
If we know the forces under which failure would occur, we can design to avoid failure. Further, a system often needs to remain close to its original shape to function properly. If we can quantify deformations, we can design the system to avoid undesirably large deformation.
3.Desirable deformation -
Deformation is desirable in some situations where it depends predictably on the forces.Some products must deform to carry out their function. They are designed to have a desired relation between the deformation and the acting forces.
For example, such products include pole vaults that flex to temporarily store energy that later propels the vaulter, mountings that accommodate motions of helicopter blades, and support springs that allow for deflection of structural members.



4.Desirable failure -
Occasionally, failure is desirable, if it occurs at a reproducible level of load.
Rarely, we sometimes deliberately want failure to occur when loads reach a predetermined level. In expensive equipment, failure can be disastrous. So, engineers design into the equipment an inexpensive extra part, which fails at a consistent force that is safely less than the main components can tolerate.
For the transmission shaft in a drive train, such a system that protects the shaft is called a torque fuse. Just as an old fashioned electric fuse breaks when the current is too high, the pins in the torque fuse break when the torque is too high.
Prediction of Deformation and Failure
↠A few very general scientific principles are needed to predict deformation and failure.
↠With very general principles, we can consider bodies with a wide range of geometries and materials, which are subjected to many types of loads.
↠Mechanics of Materials introduces these principles and applies them to bodies and loadings that can be
analyzed with relatively simple mathematics.
1.Separate out the effects of material and geometry by viewing a body as composed of many tiny elements.
↠Any body can be viewed as an assemblage of tiny, in fact infinitesimal, cubic elements. This insight allows us to separate out the effect of the body’s material from its shape.
↠Since a tiny cube is a standard shape,the relations between the cube’s deformation and the forces on it depend only on the material, for example, the particular type of ceramic, metal, plastic, or wood
These relations can be measured and described for a given material, and they are relevant to a body of any shape and size composed of that material.
2.Relate forces and deformations at the element level with those at the level of the overall structure.
↠Mechanics of materials defines stress and strain to describe force and deformation at the level of an elemental cube.
↠To determine a body’s overall deformation and potential for failure, we combine
(1) the material-specific stress–strain relations for a cubic element,
(2) equilibrium relations between forces on the body as a whole and the forces on its elements, and
(3) geometric relations between deformations of the whole body and of its elements.
3. Loaded bodies often deform in simple patterns, namely, stretching, twisting, or bending.
↠Engineers deal with deformation and failure in structures having a wide variety of shapes, materials, and loadings.
↠In mechanics of materials, we study deformation and failure primarily for simple patterns of deformation:
stretching, twisting, or bending.
↠For each pattern, the overall loading is described by equal and opposite forces or moments at the two ends.
↠The overall deformation is described by a single parameter: how much the body stretches, twists, or bends.
4. Study deflection and failure for each pattern individually, and then how they combine.
↠In mechanics of materials, we learn how the forces and deformations vary from one cubic element to another for each deformation pattern . With that information, we interrelate the overall load and deformation for that pattern, and we find the load at which failure will occur.
↠We learn how the body’s geometry (length and cross-section) and the body’s material independently affect the overall deformation and failure.
↠Faced with applications that appear complex, we must also learn to detect the presence of these simple deformation patterns, alone or, often, in combination. We typically analyze the deformations and stresses in each pattern and then combine them appropriately to find the total deformation and to determine if failure will occur.
↠With very general principles, we can consider bodies with a wide range of geometries and materials, which are subjected to many types of loads.
↠Mechanics of Materials introduces these principles and applies them to bodies and loadings that can be
analyzed with relatively simple mathematics.
1.Separate out the effects of material and geometry by viewing a body as composed of many tiny elements.
↠Any body can be viewed as an assemblage of tiny, in fact infinitesimal, cubic elements. This insight allows us to separate out the effect of the body’s material from its shape.
↠Since a tiny cube is a standard shape,the relations between the cube’s deformation and the forces on it depend only on the material, for example, the particular type of ceramic, metal, plastic, or wood
These relations can be measured and described for a given material, and they are relevant to a body of any shape and size composed of that material.
2.Relate forces and deformations at the element level with those at the level of the overall structure.
↠Mechanics of materials defines stress and strain to describe force and deformation at the level of an elemental cube.
↠To determine a body’s overall deformation and potential for failure, we combine
(1) the material-specific stress–strain relations for a cubic element,
(2) equilibrium relations between forces on the body as a whole and the forces on its elements, and
(3) geometric relations between deformations of the whole body and of its elements.
3. Loaded bodies often deform in simple patterns, namely, stretching, twisting, or bending.
↠Engineers deal with deformation and failure in structures having a wide variety of shapes, materials, and loadings.
↠In mechanics of materials, we study deformation and failure primarily for simple patterns of deformation:
stretching, twisting, or bending.
↠For each pattern, the overall loading is described by equal and opposite forces or moments at the two ends.
↠The overall deformation is described by a single parameter: how much the body stretches, twists, or bends.
4. Study deflection and failure for each pattern individually, and then how they combine.
↠In mechanics of materials, we learn how the forces and deformations vary from one cubic element to another for each deformation pattern . With that information, we interrelate the overall load and deformation for that pattern, and we find the load at which failure will occur.
↠We learn how the body’s geometry (length and cross-section) and the body’s material independently affect the overall deformation and failure.
↠Faced with applications that appear complex, we must also learn to detect the presence of these simple deformation patterns, alone or, often, in combination. We typically analyze the deformations and stresses in each pattern and then combine them appropriately to find the total deformation and to determine if failure will occur.
Statics—Forces, Subsystems,and Free Body Diagrams
For this reason, Statics, which addresses the forces on bodies in equilibrium, is a critical prerequisite to Mechanics of Materials.
The central ideas of Statics are-
1.Force - A force describes the equal and opposite mechanical interaction between two bodies, one upon the other, which often are in contact. . Since a force has a magnitude, direction, and sense, we represent it mathematically by a vector. Two forces applied to a body at the same point have the same effect as their vector sum.
2.Engineering systems of interest may consist of multiple, interconnected parts, which exert forces on each other. Any pair of contacting parts can exert forces on each other. We must be prepared to consider all such forces and to quantify those deemed necessary.
3.All subsystems of a system in equilibrium are also in equilibrium.
A system that is at rest (or at least not accelerating) is in equilibrium.
Any part or “subsystem” of a system in equilibrium is also in equilibrium.The forces on the subsystem, acting in combination, keep the subsystem in equilibrium.
4.Free Body Diagram-
A free body diagram displays all forces that affect the equilibrium of a subsystem.
In a free body diagram (FBD), we draw a subsystem and all the forces directly exerted on it by bodies external to the subsystem. The FBD is helpful because equilibrium of the subsystem is fully determined by the forces drawn in the diagram.
5.Selection of subsystems to find forces of interest -
We can choose to focus on any subsystem. We choose particular subsystems because their FBDs
contain forces of interest that we wish to determine.
Sometimes, we even consider a portion of a single part as a subsystem. This is important in mechanics of materials, because we often need to find the internal force that acts within a part,between one portion and another.
Statics—Representing Force Interactions
1.Represent forces of interaction as simply as possible.
2.In simplifying forces,consider their tendencies to cause translational and rotational acceleration.
- A single force acting on a body tends to cause translational acceleration. The force also tends to cause rotational acceleration if it produces a non-zero moment about the center of mass, G. The moment due to the force,M|G, is equal to the force,F, times the perpendicular distance, d.
- Two or more forces can still cause a rotational acceleration, even if they sum as vectors to zero net force. We sometimes represent such force combinations with a couple(often called a moment),which causes only rotational acceleration. The couple produces the same moment about any
point.
- The translational and rotational acceleration produced by any combination of forces can be
produced by one force and one couple, provided they are statically equivalent to the original
combination. Two sets of forces and couples are statically equivalent if they correspond to the same
net force and moment. We often represent a combination of forces by just a statically equivalent force and couple.
3.Represent the unknown interaction between two connected bodies by considering which motions of one body the other can resist.
Consider a pair of connected bodies. Hold one body and try to move the other body in various
ways. The first body may or may not be able to resist each motion, depending on the connection.
If a motion is resisted, the corresponding force or couple can act and must be included in the
representation of unknowns.
More specifically,
- Ask if a body can resist the connected body’s translation in some direction.
If so, then the representation of the interaction must include a force that acts in that direction. - Ask if a body can resist the connected body’s rotation about some axis.
If so, then the representation of the interaction must include a couple that acts about that axis.
4.Recall how interactions between bodies joined by common connections are represented.
Here are commonly encountered connections and how the interaction between the connected bodies is represented. We assume there is only loading in the plane (2-D).
- A cord that connects two bodies only resists each body’s translation parallel to the cord, away
from each other. Only the magnitude F is unknown. There can be only a tensile force (F>0)
parallel to the cord.
- For a roller connection, translation perpendicular to the rolled-on surface is resisted, but not parallel translation or rotation. Only the magnitude F is unknown, and the force acts
perpendicularly to the rolled-on surface.
- For a pin connection, translation in any direction is resisted, but not rotation. There can be a force in any direction in the plane but no couple. We can represent an arbitrary force in the plane with
two independent unknown force components Fx and Fy.
- .For a fixed or rigid connection, rotation and translation in any direction is resisted. There can be a force in any direction in the plane and a couple. The force magnitudes , Fx , Fy and couple magnitude M are unknown
Statics—Conditions of Equilibrium
1.A subsystem is in equilibrium if the combined effect of all external forces produces zero translational and rotational acceleration.
If there is to be no translational acceleration, the forces must sum to zero: ΣF=0
If there is to be no rotational acceleration, the moments must sum to zero: ΣM|o =0
where O is any point on or off the body.
Force and moment summation should include all external forces acting directly on the subsystem,namely, the forces drawn in the FBD.
2.Equilibrium can be imposed along coordinate axes.
Vector equilibrium conditions are equivalent to individual force summations along each of three axes:
ΣFx=0 ΣFy=0 ΣFz=0
and moment summations about each of three axes:
ΣM|Ox=0 ΣM|Oy=0 ΣM|Oz=0
The axes for the moment summations can be through different points, not all through the same point O.
If loads can be represented by forces in a single plane, then there are only three independent equilibrium equations:
ΣFx=0 ΣFy=0 ΣM|O =0
where the moment is about the z-axis (perpendicular to the x-yaxes) through any point O.
3.Be sure to account for couples correctly when imposing equilibrium conditions.
Do not include couples in the force summations: each couple has zero net force!
In moment summations, include moments due to forces and due to couples.
The moment due to a couple which acts on the subsystem is independent of the couple’s location or the point about which the moment is taken.
4.Plan out the order in which you impose equations, and consider imposing equilibrium on multiple subsystems.
When the equilibrium equations for a given subsystem are sufficient to find the unknowns, it is often efficient first to sum moments about a carefully chosen point to find one force. Then, use the force summations to find the other forces.
If a desired unknown cannot be found using a single subsystem, draw FBDs of one or more additional subsystems and impose equilibrium on them to find intermediate unknowns.












No comments:
Post a Comment